Relaxation is the return of a perturbed system to equilibrium. This is very general: this return to equilibrium may occur in different ways and due to multiple processes, affecting different physical quantities. Therefore, the concept of relaxation time has had multiple quantitative definitions in the literature. In star clusters we have two processes driving relaxation: 2-body (collisional; nonresonant) and resonant relaxation. 2-body relaxation (which is what people traditionally mean when talking about relaxation in stellar systems) is so-named in analogy to molecules colliding in a gas.
The traditional view is that a star happily moves in a straight line while occasionally a second star tugs it around in a way that statistically generates or maintains equilibrium. Moving forward from this simplified 2-body view, we can break the gravitational field into two parts: a smooth time-independent component (mean field) and a fluctuating part on top of it. 2-body relaxation is due to temporal fluctuations in the gravitational field, in globular clusters it affects all conserved quantities (energy, angular momentum direction and magnitude). Resonant relaxation, on the other hand, is a result of spatial fluctuations in the mean field, and in globular clusters it affects only the angular momentum direction.
In two papers with Bence Kocsis, we studied relaxation of physical quantities in star clusters, specifically characterizing the relative importance of resonant relaxation vs. 2-body relaxation in these systems.
In the first paper (Meiron & Kocsis 2018), concentrating on nonresonant dynamics, we made an important distinction between the concepts of relaxation and mixing. Mixing is the tendency of a distribution of a quantity x of any subpopulation in the cluster to evolve toward the distribution in the whole cluster, or “forgetting the initial conditions”. It occurs on much longer timescales than the relaxation time of x (which in the context of star cluster means the diffusion time). Both relaxation and mixing are manifestations of 2-body encounters, but there are different associated time scales. We defined a quantity called mixedness that quantifies the extent to which the initial conditions of a particular orbit have been forgotten due to collisions.
In the second paper (Meiron & Kocsis 2019), we followed star clusters using N-body simulations and found that (vector-) resonant relaxation operates efficiently in clusters with N > 104 (i.e. virtually all globular clusters). Since the distribution of orbital planes relaxes much more rapidly than the distribution of the magnitude of angular momentum and the radial action, the relaxation process reaches an internal statistical equilibrium in the corresponding part of phase space while the whole cluster is generally out of equilibrium, in a state of quenched disorder.
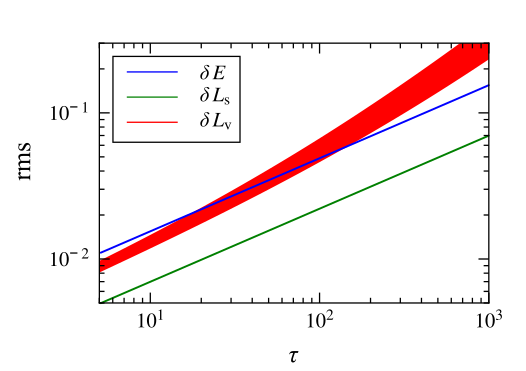
This figure from the paper shows the root-mean-square (rms) relative changes in the energy (blue) and angular momentum (magnitude in green, direction in red) as a function of time (normalized by orbital period) for nearly circular orbit in a Plummer sphere with a million stars (the orbital radius is the model’s virial radius in this case).
The evolution of energy and the angular momentum magnitude are $\sim \sqrt{\tau}$, that is perfectly consistent with random walk. The evolution of angular momentum direction though has a random walk component but also a coherent component $\sim \tau$ because of long-living torques in the system. The red line appears thick because of the relatively large possible range of the coefficient controlling the strength of the coherent drift (i.e. sometimes the torques happen to be stronger than other times).